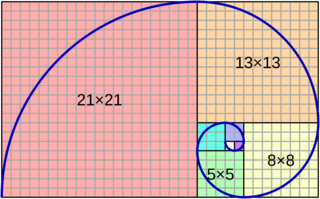
We know that the Fibonacci sequence is defined as a sequence in which each number is the sum of the two preceding numbers, i.e.:

$$ \begin{aligned} F_{0} &= 0 \\ F_{1} &= 1 \\ F_{n} &= F_{n-1} + F_{n-2} \text{ for n > 1} \end{aligned} $$

The beginning of the Fibonacci sequence is then: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

The Fibonacci sequence is closely related to the golden ratio (φ) in various ways. One relationship is that the ratio of consecutive Fibonacci numbers gets closer and closer to (i.e., converges to) φ as n increases. That is,

$$ \begin{aligned} φ &\approx \frac{F_{n+1}}{F_{n}} & \text{more precise as n increases}\\ &= \lim_{n\to\infty}\frac{F_{n+1}}{F_n} & \text{formally via limit notation} \end{aligned} $$

The golden ratio is an irrational number and therefore can't be expressed as the ratio of two integers. However, it can be expressed in the following forms and approximations:

$$ \begin{aligned} φ &= \frac{1 + \sqrt{5}}{2} & \text{as a closed-form solution} \\ &= \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}} & \text{as a nested radical} \\ &\approx 1.618033988749895 & \text{as an approximate decimal value} \\ \end{aligned} $$

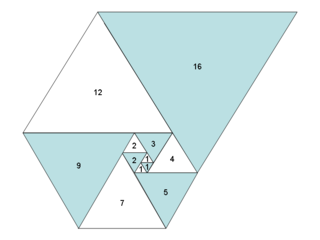
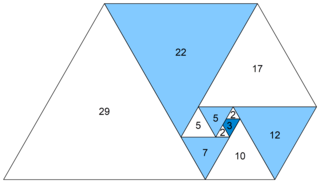
Two other sequences, very similar to the Fibonacci sequence, exhibit some similar characteristics. The Padovan sequence and the Perrin sequence are identical except for their starting points:

$$ \begin{aligned} Padovan_{0} &= 1 \\ Padovan_{1} &= 1 \\ Padovan_{2} &= 1 \\ Padovan_{n} &= Padovan_{n-2} + Padovan_{n-3} \text{ for n > 2} \end{aligned} $$

The beginning of the Padovan sequence is then: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, …

$$ \begin{aligned} Perrin_{0} &= 3 \\ Perrin_{1} &= 0 \\ Perrin_{2} &= 2 \\ Perrin_{n} &= Perrin_{n-2} + Perrin_{n-3} \text{ for n > 2} \end{aligned} $$

The beginning of the Perrin sequence is then: 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, …

These sequences are related to the plastic number (ρ) much like the Fibonacci sequence is related to the golden ratio. One relationship is that the ratio of consecutive Padovan or Perrin numbers gets closer and closer to (i.e., converges to) ρ as n increases. That is,

$$ \begin{aligned} ρ &\approx \frac{Padovan_{n+1}}{Padovan_{n}} & \text{more precise as n increases} \\ &= \lim_{n\to\infty}\frac{Padovan_{n+1}}{Padovan_n} & \text{formally via limit notation} \\ &\approx \frac{Perrin_{n+1}}{Perrin_{n}} & \text{more precise as n increases} \\ &= \lim_{n\to\infty}\frac{Perrin_{n+1}}{Perrin_n} & \text{formally via limit notation} \end{aligned} $$

The plastic number is an irrational number and therefore can't be expressed as the ratio of two integers. However, it can be expressed in the following forms and approximations:

$$ \begin{aligned} ρ &= \sqrt[3]{\frac{9+\sqrt{69}}{18}}+\sqrt[3]{\frac{9-\sqrt{69}}{18}} & \text{as a closed-form solution} \\ &= \sqrt[3]{1 + \sqrt[3]{1 + \sqrt[3]{1 + \cdots}}} & \text{as a nested radical} \\ &\approx 1.324717957244746 & \text{as an approximate decimal value} \\ \end{aligned} $$

recurrence.py

"""
This module implements several functions in order to practice with generators.
 
Function docstrings also have extended info on parameters and return values, as well as doctests,
which are a way of embedding runnable tests in docstrings.
https://docs.python.org/3/library/doctest.html
 
python -m doctest recurrence.py     # output only failed tests
python -m doctest -v recurrence.py  # verbose output
"""
 
from typing import Generator, Callable
 
 
def fibonacci() -> Generator[str, None, None]:
  """
  Yields an infinite sequence of Fibonacci numbers.
  See: https://en.wikipedia.org/wiki/Fibonacci_number
 
  >>> [fib for (idx, fib) in zip(range(10), fibonacci())]
  [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
  """
  # We did this in class, so it's good to go:
  previous, current = 0, 1
  yield previous
  yield current
  while True:
    previous, current = current, previous + current
    yield current
 
 
def padovan() -> Generator[str, None, None]:
  """
  Yields an infinite sequence of Padovan numbers.
  See: https://en.wikipedia.org/wiki/Padovan_sequence
 
  >>> [pad for (idx, pad) in zip(range(10), padovan())]
  [1, 1, 1, 2, 2, 3, 4, 5, 7, 9]
  """
  pass  # TODO
 
 
def perrin() -> Generator[str, None, None]:
  """
  Yields an infinite sequence of Perrin numbers.
  See: https://en.wikipedia.org/wiki/Perrin_number
 
  >>> [per for (idx, per) in zip(range(10), perrin())]
  [3, 0, 2, 3, 2, 5, 5, 7, 10, 12]
  """
  pass  # TODO
 
 
def phi(terms: int) -> float:
  """
  Recursively calculates the golden ratio (often denoted as the Greek letter ϕ, i.e. "phi")
  via its nested radical representation.
  See: https://en.wikipedia.org/wiki/Golden_ratio
 
  :param terms: the number of formula terms to calculate, assumed to be positive
  :return: phi calculated to the requested number of terms
 
  >>> phi(1) == 1**(1 / 2)
  True
  >>> phi(2) == (1 + 1**(1 / 2))**(1 / 2)
  True
  >>> phi(3) == (1 + (1 + 1**(1 / 2))**(1 / 2))**(1 / 2)
  True
  >>> phi(4) == (1 + (1 + (1 + 1**(1 / 2))**(1 / 2))**(1 / 2))**(1 / 2)
  True
  """
  pass  # TODO
 
 
def rho(terms: int) -> float:
  """
  Calculates the plastic number (often denoted as the Greek letter ρ, i.e. "rho")
  via its nested radical representation.
 
  :param terms: the number of formula terms to calculate, assumed to be positive
  :return: rho calculated to the requested number of terms
 
  >>> rho(1) == 1**(1 / 3)
  True
  >>> rho(2) == (1 + 1**(1 / 3))**(1 / 3)
  True
  >>> rho(3) == (1 + (1 + 1**(1 / 3))**(1 / 3))**(1 / 3)
  True
  >>> rho(4) == (1 + (1 + (1 + 1**(1 / 3))**(1 / 3))**(1 / 3))**(1 / 3)
  True
  """
  pass  # TODO
 
 
def most_precise(function: Callable):
  """
  Calls a function with successively larger positive integer arguments (starting from 1)
  until the function returns the same value twice in succession. Meant to work with
  functions like rho and phi in this module, e.g. most_precise(rho) will repeatedly call rho
  requesting more terms in the calculationuntil two successive calls return the same value.
 
  :param function: the function to call with successively larger arguments
  :return: the first repeated return value
 
  >>> most_precise_phi = most_precise(phi)
  >>> most_precise_phi == phi(32)  # nested-radical phi should hit peak precision at 32 terms
  True
  >>> most_precise_phi == (1 + 5**(1 / 2)) / 2  # closed-form solution should be equal
  True
  >>> # verify the relationship between Fibonacci sequence and phi (30 terms, within a billionth)
  >>> fib_30 = [fib for (idx, fib) in zip(range(30), fibonacci())]
  >>> abs(fib_30[-1] / fib_30[-2] - most_precise_phi) < 1e-9
  True
  >>>
  >>> most_precise_rho = most_precise(rho)
  >>> most_precise_rho == rho(24)  # nested-radical rho should hit peak precision at 24 terms
  True
  >>> most_precise_rho == ((9 - 69**(1 / 2)) / 18)**(1 / 3) + (
  ...       (9 + 69**(1 / 2)) / 18)**(1 / 3)  # closed-form solution should be equal
  True
  >>> # verify the relationship between the Padovan/Perrin sequences and rho
  >>> padovan_60 = [pad for (idx, pad) in zip(range(60), padovan())]
  >>> abs(padovan_60[-1] / padovan_60[-2] - most_precise_rho) < 1e-9
  True
  >>> perrin_60 = [per for (idx, per) in zip(range(60), perrin())]
  >>> abs(perrin_60[-1] / perrin_60[-2] - most_precise_rho) < 1e-9
  True
  """
  pass  # TODO

Submit recurrence.py via turnin.