Table of Contents

cs20pf22as08: Recursive Fractal Generation

Goals

Prerequisites

This assignment requires familiarity with the lecture materials presented in class through week 08.

Background

The Sierpiński Triangle is a fractal (i.e., a self-similar pattern) with the overall shape of a triangle, subdivided recursively into smaller triangles.

A Sierpiński triangle

In other words, a Sierpiński triangle is composed of three Sierpiński triangles, each of which is composed of three Sierpiński triangles, and so on…

An animation of "zooming in" on a Sierpiński triangle

The Pillow Library and Image Coordinates

We have the Pillow imaging library available on our Python installation on the server. It presents a friendly interface for creating and modifying images.

In order to understand how to draw lines on an image, you must first understand the coordinate system used in images. It's a straightforward 2D Cartesian coordinate system. As shown in the image below, the main difference from normal x/y-plane coordinates is that the origin (coordinate (0, 0)) is at the upper-left corner, and all coordinate values are positive, where the x axis is increasingly positive in a rightward direction and the y axis is increasingly positive in a downward direction:

Image coordinate system

Here is some code that uses Pillow to create a 320×240-pixel RGBA image initially filled with the color red, draws a black line from the origin (upper-left corner) to the bottom-right corner, and emits the image in PNG format on standard output:

pillow_demo.py
import sys
from PIL import Image, ImageDraw
 
image = Image.new('RGBA', (320, 240), 'red')
draw = ImageDraw.Draw(image)
draw.line(((0, 0), (319, 239)), fill='black')
image.save(sys.stdout, 'PNG')

Were you execute the following command on the server, the image would be placed in file ~/public_html/pillow_demo.png and therefore be available via the URL jeff.cis.cabrillo.edu/~/pillow_demo.png 

python pillow_demo.py >~/public_html/pillow_demo.png

The image itself should look as follows:

Image resulting from the above example

Assignment

You shall write a Python program that accepts 5 command-line arguments and uses Pillow to generate a RGBA PNG image of a Sierpiński triangle on standard output.

The command-line arguments shall consist of the following:

  1. The integer width (in pixels) of the image
  2. The integer height (in pixels) of the image
  3. The background color to fill the image with initially
  4. The foreground (drawing) color for drawing the Sierpiński triangle
  5. The minimum area (in pixels) that a triangle must have in order to be drawn, as a decimal floating-point value

The vertices for the outermost Sierpiński triangle shall be the middle of the top row, the bottom left corner, and the bottom right corner of the image.

You may assume that the values of all command-line arguments are valid/sane.

Demo

For testing purposes you can fill out the fields below with appropriate argument values to generate the expected resulting image: 





Demo image displayed here, or nothing if invalid arguments were provided.










Tips




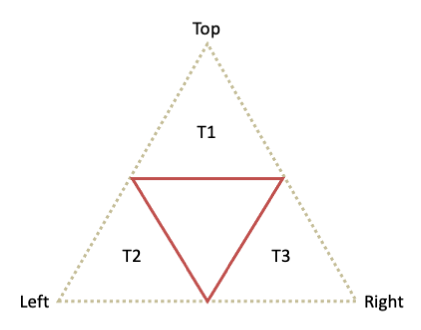
Drawing a Sierpiński triangle is easily accomplished in a recursive manner. You will probably want to implement a recursive function that accepts arguments indicating three points of a triangle. Consider them to be Top, Left and Right in the diagram below. The algorithm would then consist of the following steps:



    

  1.  Compute the midpoints between Top and Left, Top and Right, and Left and Right. Don't round any numbers! Pillow will be happy to round coordinates to the nearest pixel, so keep your arithmetic precise to get the most precise vertex coordinates.
    

    2. 

  2.  If the area of the triangle connecting those three midpoints is smaller than the predetermined minimum area, stop the process (i.e., return—this is a base case).
    

    3. 

  3.  Otherwise:
    

      

    1.  Draw a triangle by drawing three lines connecting the three midpoints.
      

      2. 

    2.  Perform recursive calls to this function to draw each of the three Sierpiński subtriangles (i.e., T1, T2 and T3 in the diagrams below). These are recursive steps.
      

      3. 

    

    4. 






Given three starting vertices, compute the midpoints between them and draw a triangle connecting those midpoints.






Draw a triangle between the midpoints of the given vertices.






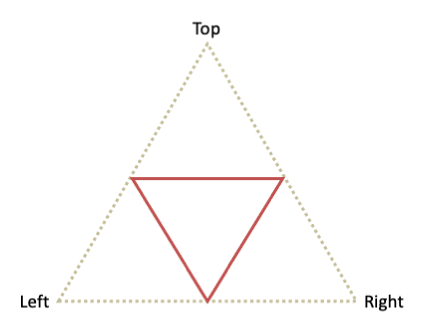
Make recursive calls to draw Sierpiński triangles in the upper (“T1”), left (“T2”), and right (“T3”) corners of the triangle.






Make recursive calls to draw subtriangles T1, T2, and T3.






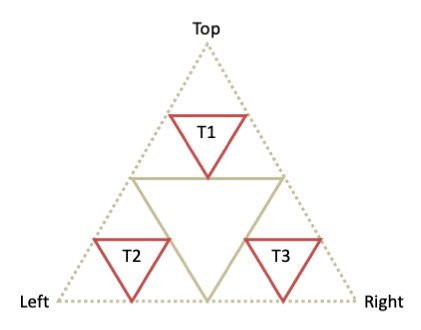
Continue the process until reaching a base case (i.e. the area of the triangle would be smaller than the specified minimum).






Draw a triangle between the midpoints of the given vertices.






Submission




Submit your source-code file(s) via turnin.






 Feedback Robot





This project has a feedback robot that will run some tests on your submission and provide you with a feedback report via email within roughly one minute.





Please read the feedback carefully.





Due Date and Point Value





Due at 23:59:59 on the date listed on the syllabus.





Assignment 08 is worth 60 points.



Possible point values per category:
---------------------------------------
Correct output                       60
Possible deductions:
  Style and practices            10–20%
Possible extra credit:
  Submission via Git                 5%
---------------------------------------