Table of Contents
cs19f22as10: Recursion Regarding Recurrence Relations
Goals
- Practice with recursion in C++.
- Consider some notable mathematical sequences and their relationships to some special numbers.
Prerequisites
This assignment requires familiarity with the lecture materials presented in class through week 10.
Background
Fibonacci Numbers and the Golden Ratio
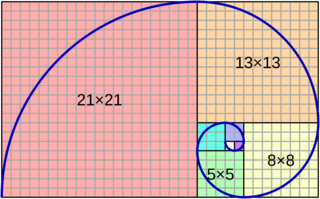
We know that the Fibonacci sequence is defined as a sequence in which each number is the sum of the two preceding numbers, i.e.:
$$ \begin{aligned} F_{0} &= 0 \\ F_{1} &= 1 \\ F_{n} &= F_{n-1} + F_{n-2} \text{ for n > 1} \end{aligned} $$
The beginning of the Fibonacci sequence is then: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
The Fibonacci sequence is closely related to the golden ratio (φ) in various ways. One relationship is that the ratio of consecutive Fibonacci numbers gets closer and closer to φ as n increases. That is,
$$ \begin{aligned} φ &\approx \frac{F_{n+1}}{F_{n}} & \text{more precise as n increases}\\ &= \lim_{n\to\infty}\frac{F_{n+1}}{F_n} & \text{formally via limit notation} \end{aligned} $$
The golden ratio is an irrational number and therefore can't be expressed as the ratio of two integers. However, it can be expressed in the following forms and approximations:
$$ \begin{aligned} φ &= \frac{1 + \sqrt{5}}{2} & \text{as a closed-form solution} \\ &= \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}} & \text{as a nested radical} \\ &\approx 1.618033988749895 & \text{as an approximate decimal value} \\ \end{aligned} $$
Padovan and Perrin Numbers and the Plastic Number
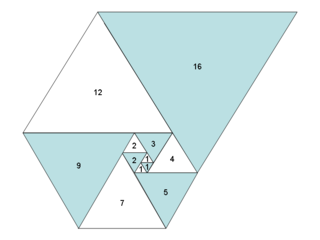
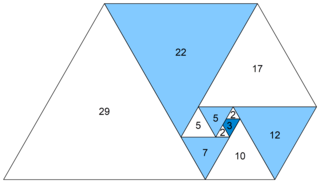
Two other sequences, very similar to the Fibonacci sequence, exhibit some similar characteristics. The Padovan sequence and the Perrin sequence are identical except for their starting points:
$$ \begin{aligned} Padovan_{0} &= 1 \\ Padovan_{1} &= 1 \\ Padovan_{2} &= 1 \\ Padovan_{n} &= Padovan_{n-2} + Padovan_{n-3} \text{ for n > 2} \end{aligned} $$
The beginning of the Padovan sequence is then: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, …
$$ \begin{aligned} Perrin_{0} &= 3 \\ Perrin_{1} &= 0 \\ Perrin_{2} &= 2 \\ Perrin_{n} &= Perrin_{n-2} + Perrin_{n-3} \text{ for n > 2} \end{aligned} $$
The beginning of the Perrin sequence is then: 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, …
These sequences are related to the plastic number (ρ) much like the Fibonacci sequence is related to the golden ratio. One relationship is that the ratio of consecutive Padovan or Perrin numbers gets closer and closer to ρ as n increases. That is,
$$ \begin{aligned} ρ &\approx \frac{Padovan_{n+1}}{Padovan_{n}} & \text{more precise as n increases} \\ &= \lim_{n\to\infty}\frac{Padovan_{n+1}}{Padovan_n} & \text{formally via limit notation} \\ &\approx \frac{Perrin_{n+1}}{Perrin_{n}} & \text{more precise as n increases} \\ &= \lim_{n\to\infty}\frac{Perrin_{n+1}}{Perrin_n} & \text{formally via limit notation} \end{aligned} $$
The plastic number is an irrational number and therefore can't be expressed as the ratio of two integers. However, it can be expressed in the following forms and approximations:
$$ \begin{aligned} ρ &= \sqrt[3]{\frac{9+\sqrt{69}}{18}}+\sqrt[3]{\frac{9-\sqrt{69}}{18}} & \text{as a closed-form solution} \\ &= \sqrt[3]{1 + \sqrt[3]{1 + \sqrt[3]{1 + \cdots}}} & \text{as a nested radical} \\ &\approx 1.324717957244746 & \text{as an approximate decimal value} \\ \end{aligned} $$
Assignment
You shall define six functions in a header file named cs19_recurrence.h as described in the skeleton code below:
- cs19_recurrence.h
#ifndef _CS19_RECURRENCE_H_ #define _CS19_RECURRENCE_H_ #include <gmpxx.h> #include <cmath> #include <unordered_map> namespace cs19 { /** * Recursively calculates index i of the Fibonacci sequence. * * @see https://en.wikipedia.org/wiki/Fibonacci_number * @param i the requested index * @param memoized whether to perform memoized recursion * @return index i of the Fibonacci sequence */ mpz_class fibonacci(unsigned i, bool memoized = false) { // We covered this in class, so might as well just include the code here. if (i < 2) return i; if (memoized) { static std::unordered_map<unsigned, mpz_class> memos; auto memo = memos.find(i); if (memo == memos.end()) { mpz_class result = fibonacci(i - 1, true) + fibonacci(i - 2, true); memos[i] = result; return result; } else { return memo->second; } } return fibonacci(i - 1) + fibonacci(i - 2); } /** * Recursively calculates the golden ratio (often denoted as the Greek letter φ ("phi") via its * nested radical representation. * * @see https://en.wikipedia.org/wiki/Golden_ratio * @param terms the number of terms in the nested radical to compute (assumed to be >= 1) * @return phi calculated via the requested number of nested-radical terms */ double phi(unsigned terms) { // TODO } /** * Recursively calculates the plastic number (often denoted as the Greek letter ρ ("rho")) via its * nested radical representation. * * @see https://en.wikipedia.org/wiki/Plastic_number * @param terms the number of terms in the nested radical to compute (assumed to be >= 1) * @return rho calculated via the requested number of nested-radical terms */ double rho(unsigned terms) { // TODO } /** * Calls a function with successively larger integer arguments (starting from 1) until the function * returns the same value twice in succession, and returns that value. Meant to work with functions * like rho and phi in this assignment, e.g. `most_precise(rho)` will repeatedly call rho (`rho(1)`, * `rho(2)`, `rho(3)`, etc.) requesting more levels of recursion until two successive calls return * the same value. * * @tparam Function a function with one parameter of type `unsigned` and a return type of `double` * @param fun the function to call with successively larger arguments * @return the first repeated return value */ template <typename Function> double most_precise(Function func) { // TODO } /** * Recursively calculates index i of the Padovan sequence. * @see https://en.wikipedia.org/wiki/Padovan_sequence * * @param i the requested index (starting from 0) * @param memoized whether to perform memoized recursion * @return index i of the Padovan sequence */ mpz_class padovan(unsigned i, bool memoized = false) { // TODO } /** * Recursively calculates index i of the Perrin sequence. * @see https://en.wikipedia.org/wiki/Perrin_number * * @param i the requested index (starting from 0) * @param memoized whether to perform memoized recursion * @return index i of the Perrin sequence */ mpz_class perrin(unsigned i, bool memoized = false) { // TODO } } // namespace cs19 #endif // _CS19_RECURRENCE_H_
Memoization
For the functions that offer memoized recursion, follow my model of memoization in the cs19::fibonacci() function, i.e. use a static map as a local variable in the function.
Testing
Here are a few assertion tests to get you started.
- recurrence_tests.cpp
#include <cassert> #include <cmath> #include "cs19_recurrence.h" int main() { constexpr double EPSILON = 1e-15; // threshold for precision // test recursive phi assert(cs19::phi(1) == std::sqrt(1)); assert(cs19::phi(2) == std::sqrt(1 + std::sqrt(1))); assert(cs19::phi(3) == std::sqrt(1 + std::sqrt(1 + std::sqrt(1)))); assert(cs19::phi(4) == std::sqrt(1 + std::sqrt(1 + std::sqrt(1 + std::sqrt(1))))); double most_precise_phi = cs19::most_precise(cs19::phi); assert(most_precise_phi == cs19::phi(32)); // # nested-radical cs19::phi converges at 32 terms assert(std::abs(most_precise_phi - (1 + std::sqrt(5)) / 2) < EPSILON); // closed-form solution // verify the relationship between Fibonacci sequence and phi (30 terms is within a billionth) assert(std::abs(cs19::fibonacci(30).get_d() / cs19::fibonacci(29).get_d() - most_precise_phi) < 1e-9); // test cs19::Padovan and cs19::Perrin sequences assert(cs19::padovan(7) == 5 && cs19::padovan(8) == 7 && cs19::padovan(9) == 9); assert(cs19::perrin(7) == 7 && cs19::perrin(8) == 10 && cs19::perrin(9) == 12); // # test recursive rho assert(cs19::rho(1) == std::cbrt(1)); assert(cs19::rho(2) == std::cbrt(1 + std::cbrt(1))); assert(cs19::rho(3) == std::cbrt(1 + std::cbrt(1 + std::cbrt(1)))); assert(cs19::rho(4) == std::cbrt(1 + std::cbrt(1 + std::cbrt(1 + std::cbrt(1))))); double most_precise_rho = cs19::most_precise(cs19::rho); assert(most_precise_rho == cs19::rho(23)); // nested-radical rho hits peak precision at 23 terms // ensure closed-form solution is acceptably close assert(std::abs(most_precise_rho - (std::cbrt((9 - std::sqrt(69)) / 18) + std::cbrt((9 + std::sqrt(69)) / 18))) < EPSILON); // # verify the relationship between the Padovan/Perrin sequences and rho assert(abs(cs19::padovan(52) / cs19::padovan(51) - most_precise_rho) < 1e-9); assert(abs(cs19::perrin(52) / cs19::perrin(51) - most_precise_rho) < 1e-9); }
Submission
Submit cs19_recurrence.h via turnin.
 Feedback Robot
Feedback Robot
This project has a feedback robot that will run some tests on your submission and provide you with a feedback report via email within roughly one minute.
Please read the feedback carefully.
Due Date and Point Value
Due at 23:59:59 on the date listed on the syllabus.
Assignment 10 is worth 60 points.
Possible point values per category: --------------------------------------- phi() 12 rho() 12 padovan() 12 perrin() 12 most_precise() 12 Possible deductions: Imprecise recursion/call counts 50% Style and practices 10–20% Possible extra credit: Submission via Git 5% ---------------------------------------
